Segitiga dan Bangun Datar
1. Segitiga
SOAL;
Contoh soal dalam video di atas, untuk soal silakan lihat di bagian bawah.
1. Segitiga
A. Pengertian Segitiga dan Rumus Segitiga
Segitiga adalah bangun datar yang terdiri dari 3 sisi garis lurus dengan 3 titik sudut yang berjumlah 180º. Sejak tahun 300 SM, Euclid menemukan konsep bahwa jumlah ketiga sudut segitiga adalah 180º. Hal ini memberikan kontribusi yang besar dalam konsep bangun datar, seperti mencari panjang sisi dan panjang sudut.
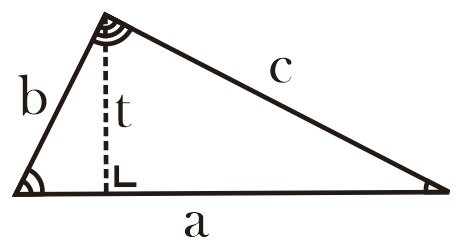
Keterangan:
a = alas
t = tinggi, tinggi segitiga membentuk sudut 90° terhadap alasnya.
b, c = adalah sisi lain segitiga
B. Rumus Segitiga
| Nama | Rumus |
|---|---|
| Luas (L) | L = ½ × a × t |
| Keliling (Kll) | Kll = a + b + c |
| Tinggi (t) | t = (2 × Luas) ÷ a |
| Alas (a) | a = (2 × Luas) ÷ t |
C. Jenis-jenis Segitiga
Jenis-jenis segitiga secara umum dapat diketahui dari panjang sisi dan besar sudutnya,
1. Jenis Segitiga Berdasarkan Panjang Sisi
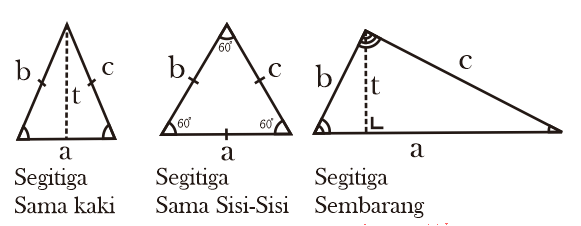
Berdasarkan Panjang sisinya segitiga dapat dibedakan menjadi 3 yaitu segitiga sama sisi, segitiga sama kaki, dan segitiga sembarang.
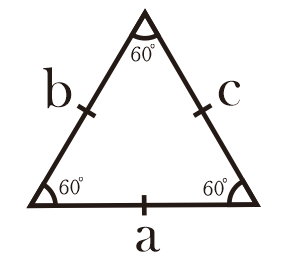
1.a. Segitiga Sama Sisi (Equilateral Triangle)
Segitiga sama sisi adalah segitiga yang ketiga sisinya mempunyai panjang sama yang menyebabkan ketiga sudutnya mempunyai ukuran 60º.
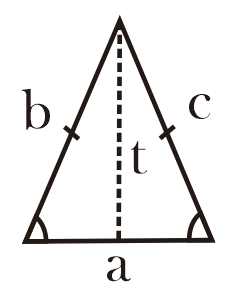
1.b. Segitiga Sama Kaki (Isosceles Triangle)
Segitiga sama kaki adalah segitiga yang mempunyai 2 sisi sama panjang yang menyebabkan 2 sudutnya memiliki besar yang sama.
1.c. Segitiga Sembarang (scalene triangle)
Segitiga sembarang adalah segitiga dengan ketiga panjang sisinya berbeda-beda, sehingga ketiga besar sudutnya juga berbeda-beda.
2. Jenis Segitiga Berdasarkan Besar Sudutnya
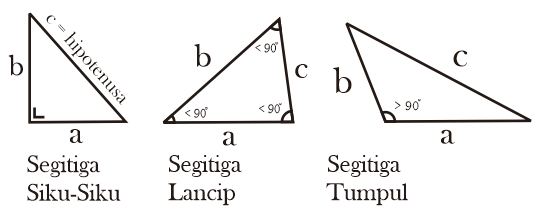
Berdasarkan besar sudutnya segitiga dapat dibedakan menjadi 3 yaitu segitiga siku-siku, segitiga lancip, dan segitiga tumpul.
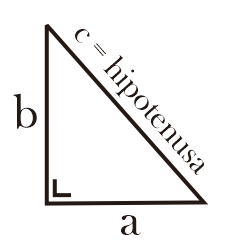
2.a. Segitiga Siku-Siku (Right Triangle)
Segitiga siku-siku adalah segitiga yang salah satu sudutnya membentuk sudut siku-siku (90º). Pada segitiga siku-siku, 2 sisinya akan membentuk sudut 90º. Sisi yang tidak membentuk sudut siku-siku disebut sisi miring (hipotenusa).
2.b. Segitiga Lancip (Acute Triangle)
Segitiga lancip adalah segitiga yang masing-masing sudut besarnya kurang dari 90°.
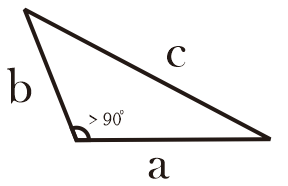
2.c. Segitiga Tumpul (Obtuse Triangle)
Segitiga tumpul adalah segitiga yang salah satu besar sudutnya lebih dari 90°.
CONTOH SOAL;SOAL;
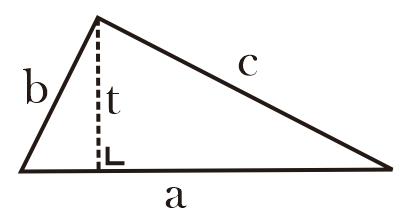
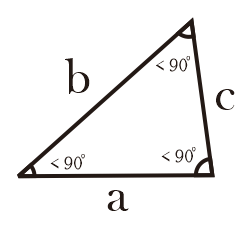


Komentar
Posting Komentar